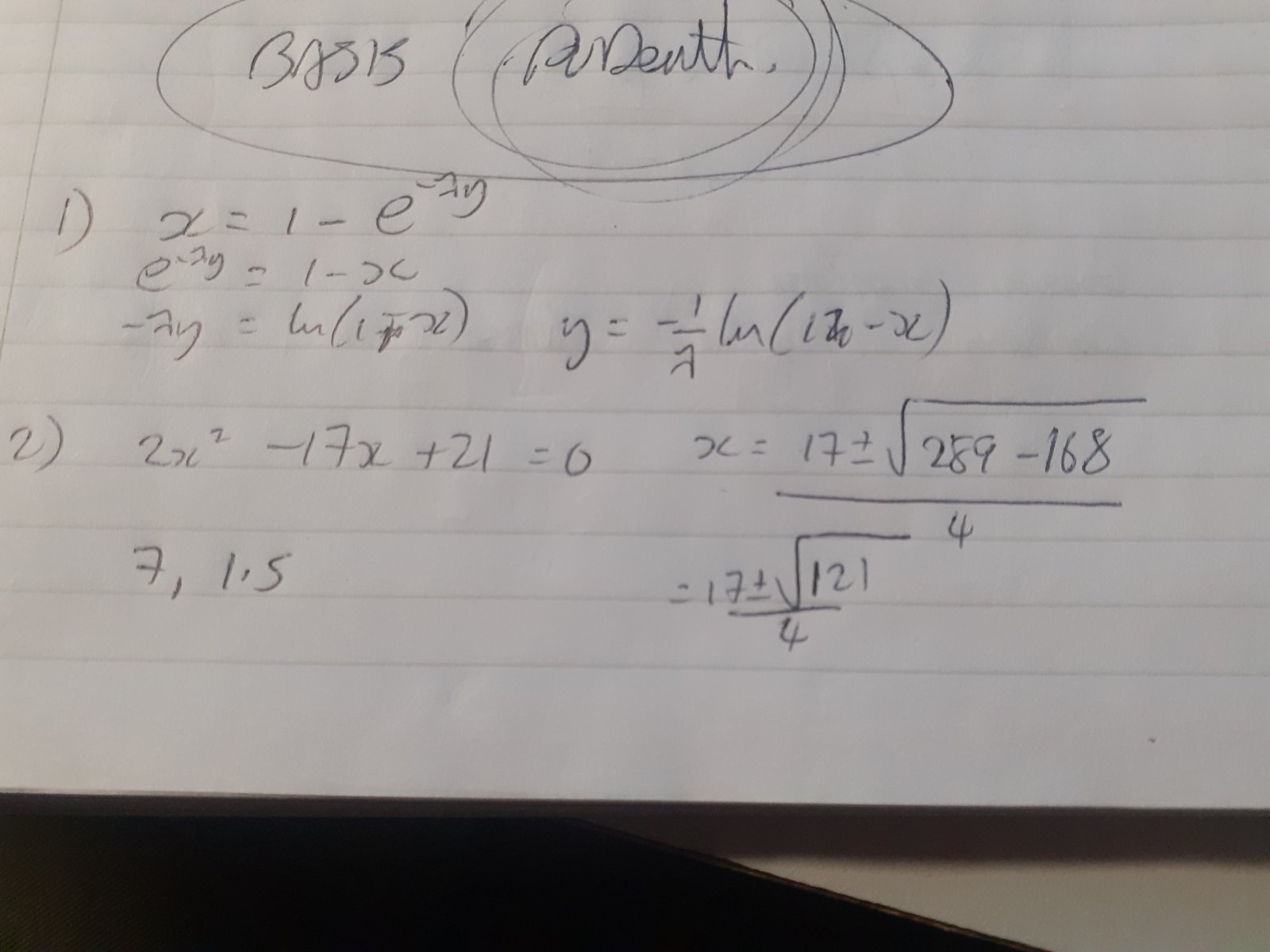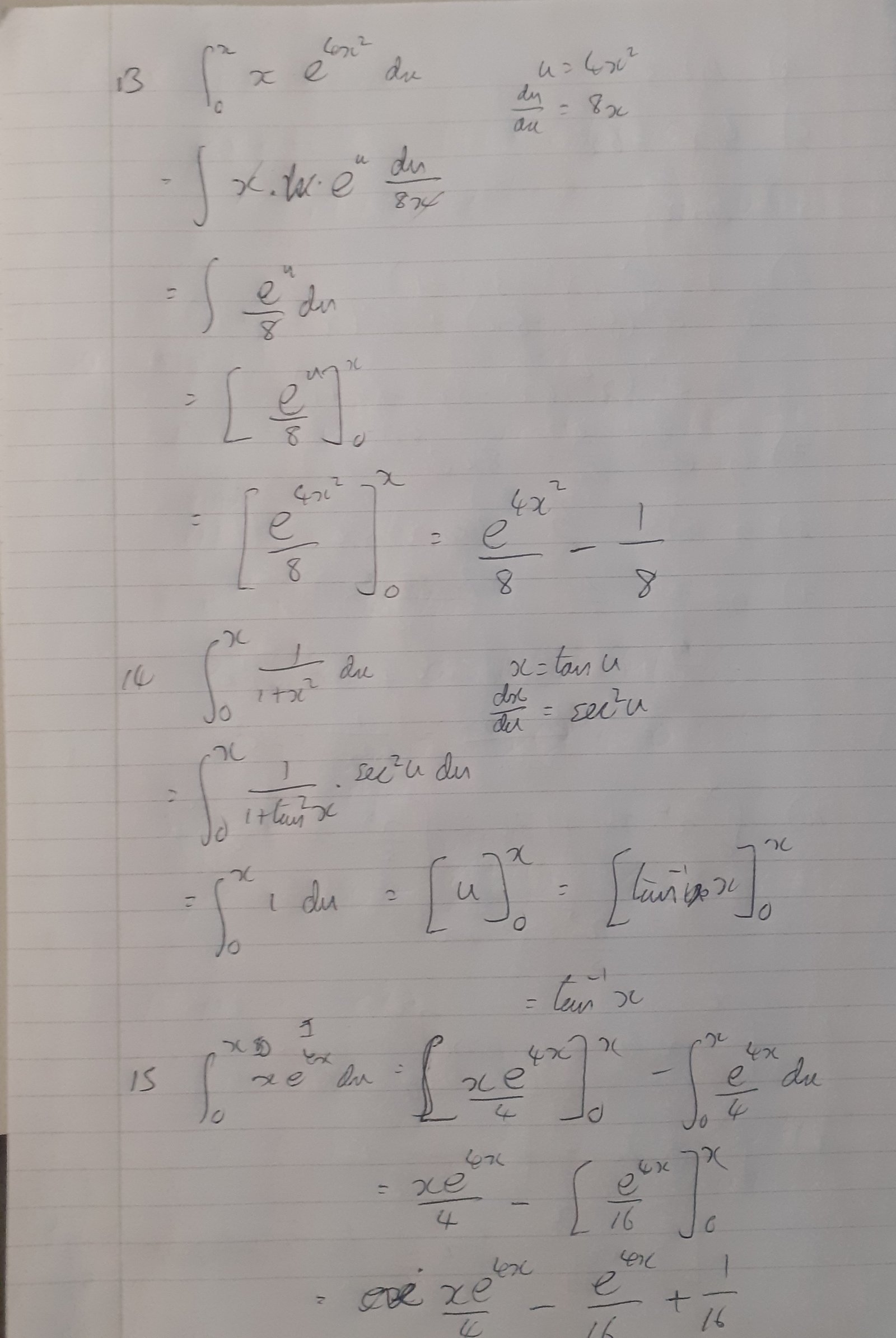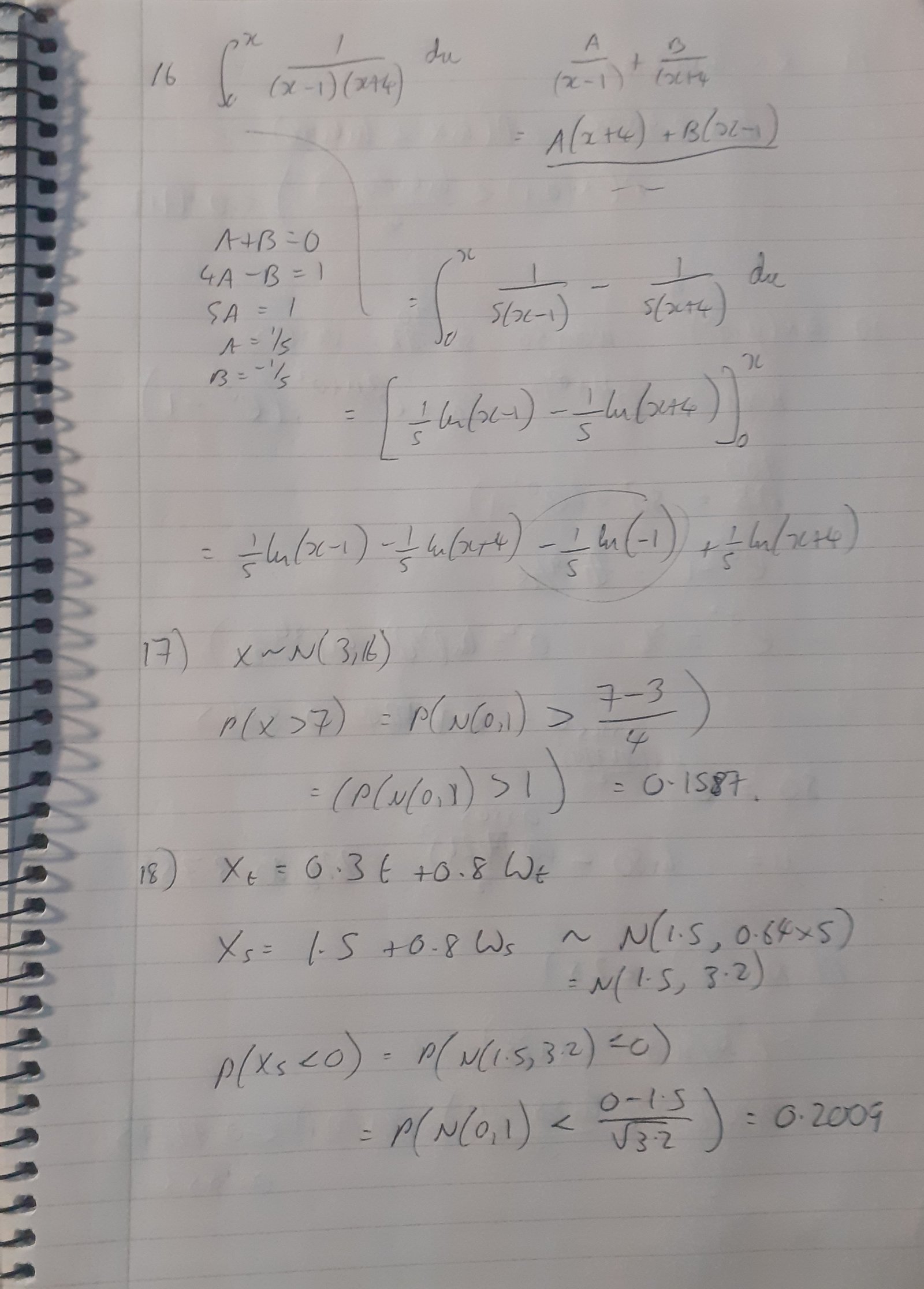Algebra
Changing the Subject of a Formula
1) Make $y$ the subject of the formula $x = 1 - e^{-\lambda y}$
Solving Quadratic Equations
2) Find the values of $x$ for which $2x^2-17x +21=0$
Factorising higher order polynomials
3) Find the values of $x$ for which $x^3-6x^2+11x=6$
Calculus
Differentiation of polynomials, exponentials and trigonometric functions
4) Evaluate $\frac{d}{dx}(x^4-3x^2+1)$
5) Evaluate $\frac{d}{dx}(sin x)$
Product Rule
6) Evaluate $\frac{d}{dx}(e^x \times (x^4-3x^2+1))$
Function of a function
7) Evaluate $\frac{d}{dx}(e^{4x^2})$
8) Evaluate $\frac{d}{dx}(sin^2x)$
9) Evaluate $\frac{d}{dx}(tan x)$
Integration of polynomials, exponentials and trigonometric functions
10) Evaluate $\displaystyle\int_0^x x^4-3x^2+1 dx$
11) Evaluate $\displaystyle\int_0^x cos x dx$
12) Evaluate $\displaystyle\int_1^x ln x dx$
Substitutions
13) Evaluate $\displaystyle\int_0^x x \times e^{4x^2} dx$
14) Evaluate $\displaystyle\int_0^x \frac{1}{1+x^2} dx$
Integration by Parts
15) Evaluate $\displaystyle\int_0^x x \times e^{4x} dx$
Use of partial fractions
16) Evaluate $\displaystyle\int_0^x \frac{1}{(x-1)(x+4)} dx$
Statistics
17) Calculate the probability that a random variable $X \sim N(3,16)$ is greater than 7
18) A random variable is defined by $X_t = 0.3t + 0.8W_t$ calculate the probability that $X_5 \lt 0$
19) Calculate the probability that a random variable $X \sim ln N(3,16)$ is less than 40,000
20) A lognormal random variable has mean 50 and standard deviation 30. Calculate the probability that a value taken from this distribution is less than 25
21) A coin is tossed 10 times. What is the probability that there will be a run of at least 3 heads at some point
22) 5 people play golf and divide themselves into 2 teams of 2 and one person plays for himself. How many different arrangements are there
Solutions
Please note that these solutions (as well as the questions) contain the very bad habit of not using a proper dummy variable inside integrals e.g. $\displaystyle\int_0^x \frac{1}{(x-1)(x+4)} dx$ instead of $\displaystyle\int_0^x \frac{1}{(u-1)(u+4)} du$. Please don't copy this!